Peut-on gagner à coup sûr à pile ou face ?
Ode aux mathématiques. Parce qu’elles sont partout, qu’elles servent à tout, tout le temps. Et que ce n’est pas si difficile de ne plus les détester. La preuve.
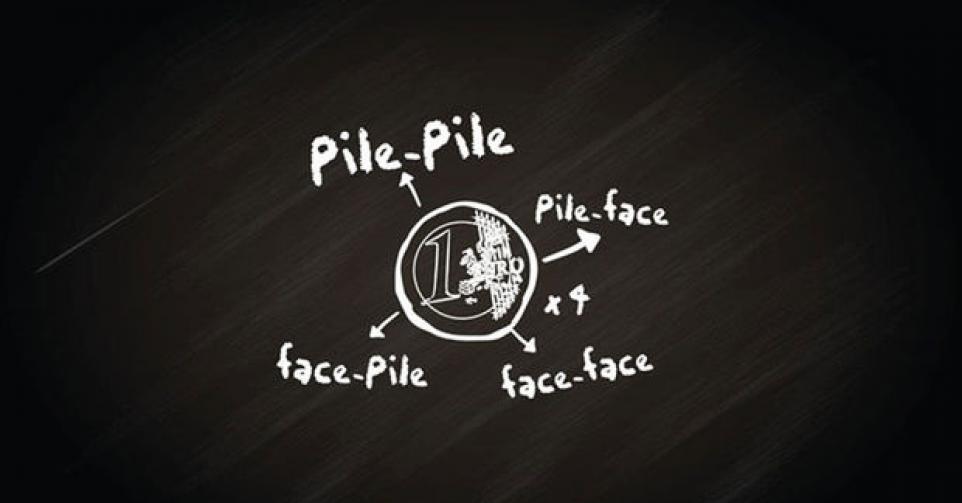
La compréhension de la théorie des probabilités s’est faite progressivement, au départ du désir de gagner aux jeux de hasard. Jouons à pile ou face avec une pièce bien équilibrée. Au début, tout est simple : lorsqu’on lance la pièce, elle a une chance sur deux de tomber côté pile et une sur deux de tomber côté face. Cela résume le fait que si on joue de très nombreuses fois, on obtiendra à peu près autant de côtés pile que de côtés face. Jouons maintenant deux fois d’affilée. On a quatre résultats possibles avec la même probabilité : (pile-pile), (pile-face), (face-pile), (face-face). On observe qu’on a deux pile avec la probabilité un quart, de même pour deux face, et qu’on a un pile et un face avec la probabilité un demi. Dans ces calculs, la somme des probabilités de tous les événements vaut toujours 1. Jouons trois fois : on a trois fois pile avec la probabilité un huitième, de même pour trois fois face, et une probabilité 3/8 pour deux fois pile et une fois face ou pour deux fois face et une fois pile.
On peut continuer ainsi et, par exemple, calculer la probabilité d’une série de résultats ne donnant que des côtés pile. A chaque nouveau jet, on divise par deux la probabilité de n’avoir que des côtés pile, puisqu’on ajoute un résultat avec soit pile soit face. On a successivement oe, OE, 1/8, 1/16, 1/32, 1/64 et après dix jets 1/(2)10 = 1/1 024 – moins d’une chance sur mille d’avoir dix pile d’affilée, c’est à dire un événement très rare.
Cela a donné lieu à une incompréhension qui a la vie dure : si on vient d’avoir une longue succession de pile (par exemple neuf), aura-t-on probablement un face au jet suivant puisqu’il est très rare de n’avoir que des pile (seulement une chance sur mille) ?
Cette idée vient assez naturellement à un joueur, qui pourrait en tenir compte dans ses mises, en jouant face quand pile est sorti plusieurs fois d’affilée. Aujourd’hui, d’innombrables sites Internet annoncent des manières de gagner à coup sûr basées sur la même idée.
Or, cette idée est fausse : quand on jette une pièce, elle n’a aucun souvenir des jets précédents.
Comment concilier les deux idées ? Imaginons qu’on ait obtenu neuf fois pile d’affilée. La probabilité d’en avoir dix n’est qu’un millième, or la probabilité d’avoir un pile au dixième jet est un demi.
En fait, la vraie question ici est : » Etant donné que les neuf premiers jets ont tous donné des pile (c’est une condition), quelle est la probabilité d’avoir un dixième pile ? » La réponse est un demi, et ne mène à aucune contradiction. Cette notion de » probabilité conditionnelle » s’avère cruciale dans la théorie des probabilités.
On peut aussi noter que la probabilité est une limite sur un grand nombre d’essais. Si on joue encore mille fois, les dix premières seront noyées dans la masse.
Historiquement, les recherches sur les jeux et la probabilité ont commencé avec des travaux de Cardano (1564), Galilée (1612), puis Pascal et Fermat (à partir de 1654) et Jacques Bernoulli (1713).
Pour l’anecdote, le 18 août 1913, au casino de Monte-Carlo, le noir est sorti 26 fois d’affilée, un événement qui ne se produit qu’une fois sur 67 108 864 et qui a coûté cher à ceux qui misaient de plus en plus sur le rouge.
Vous avez repéré une erreur ou disposez de plus d’infos? Signalez-le ici