Testez-vous

Les questions ci-dessous sont issues de l’épreuve éliminatoire de l’Olympiade mathématique belge 2017, organisée par la Société belge des professeurs de mathématiques d’expression française. Elles sont réparties en trois catégories, selon les années d’enseignement. Chaque année, environ 25 000 élèves y participent.

Niveau mini (1re et 2e secondaires)

1. 1,5 + 2,5 x 4 – 2,5 =

a. 5,25

b. 6

c. 9

d. 13,5

e. 14

2. Bruno vend le quart de ses pommes ; il lui en reste 15. Combien avait-il de pommes ?

3. On écrit, en bloc et de manière répétée, toujours dans le même ordre, les cinq premières lettres de l’alphabet : ABCDEABCDEABCDE… Quelle est la 2017e lettre qui sera écrite ?

a. A

b. B

c. C

d. D

e. E

4. La somme de trois nombres naturels consécutifs vaut 63. Que vaut leur produit ?

a. 6 840

b. 7 980

c. 9 240

d. 9 261

e. 10 626

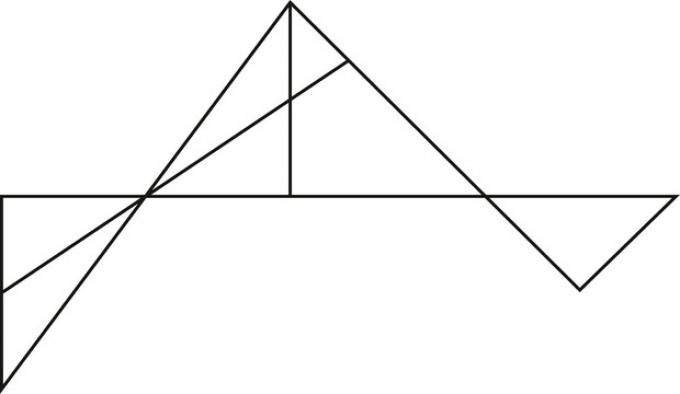
5. Combien y a-t-il de triangles dans la figure ci-dessous ?

a. 7

b. 11

c. 12

d. 13

e. 14

6. Un réservoir d’essence est rempli au sixième de sa capacité. Si on ajoute 2 litres à son contenu, il se trouve être rempli au quart de sa capacité. Quelle est, en litres, la capacité totale de ce réservoir ?

7. Le prix d’un produit dérivé du pétrole a augmenté de 60 % durant l’année 1973. Pour revenir à sa valeur initiale, ce prix devrait baisser de :

a. 70 %

b. 62,5 %

c. 60 %

d. 40 %

e. 37,5 %

8. Le périmètre d’un rectangle est de 120 cm. Si on triple sa largeur, on obtient sa longueur augmentée de 4 cm. Quelle est, en centimètres, la longueur de ce rectangle ?

a. 16

b. 22

c. 44

d. 46

e. 89

9. Mère-grand adore les devinettes. Lorsqu’on lui demande son âge, elle répond cette année :  » L’an prochain, mon âge sera divisible par 2 ; dans deux ans, mon âge sera divisible par 3 ; dans trois ans, mon âge sera divisible par 4 ; dans quatre ans, mon âge sera divisible par 5 ; et j’ai moins de 97 ans !  » Quel est l’âge de mère-grand, en années ?

a. 57

b. 58

c. 59

d. 61

e. 91

Niveau midi (3e et 4e secondaires)

1. Laquelle des expressions suivantes représente le double du cube de l’opposé de 0,1 ?

a. (2. 0,1)3

b. 23. (0,1)

c. (2. (0,1)3

d. 2. (-0,1)3

e. -23. (0,1)

2. Si x2 + 5x + 6 = 20, que vaut 3×2 + 15x+ 17 ?

3. Dans une classe, tous les élèves apprennent au moins une langue germanique : 17 le néerlandais, 18 l’allemand et 7 les deux. Combien y a-t-il d’élèves dans la classe ?

a. 21

b. 28

c. 35

d. 42

e. une autre réponse

4. Un professeur calcule la moyenne arithmétique des notes de ses 100 élèves pour une interrogation notée sur 20 points. Laquelle des propositions suivantes est vraie ?

a. Si 51 élèves ont obtenu des notes supérieures à 10, alors la moyenne est supérieure à 10.

b. Si 50 élèves ont obtenu la note 19, alors la moyenne est supérieure à 10.

c. Si la moyenne est supérieure à 10, alors les notes des élèves sont toutes supérieures à 10.

d. Si les notes des élèves sont toutes supérieures à 10, alors la moyenne est supérieure à 10.

e. Aucune des propositions précédentes n’est vraie.

5. Pour constituer une équipe de 7 joueurs, un sélectionneur doit choisir parmi 9 joueurs ; combien d’équipes différentes peut-il former ?

a. 7

b. 9

c. 36

d. 63

e. 72

6. si x2 + y2 = 42 et x + y = 8, que vaut xy ?

a. 7

b. 8

c. 9

d. 10

e. 11

7. Quel est le produit de tous les diviseurs naturels de 144 ?

a. 128

b. 1210

c. 1215

d. 1216

e. 1217

8. La somme des aires de deux carrés vaut 818. Le produit de la diagonale de l’un par la diagonale de l’autre vaut 782. Quelle est la longueur du côté du plus grand carré ?

9. Quand les longueurs des côtés d’un carré sont augmentées de 7 m, son aire augmente de 511 m2. Quelle est, en mètres, la longueur du côté du carré initial ?

a. 29,5

b. 33

c. 36,5

d. 40

e. 462

Niveau maxi (5e et 6e secondaires)

1. Des deux affirmations S’il pleut, je prends mon parapluie et Si je ne prends pas mon imperméable, alors je ne prends pas mon parapluie, il résulte que :

a. si je prends mon parapluie, alors il pleut

b. s’il pleut, je prends mon imperméable

c. si je prends mon imperméable, alors je prends mon parapluie

d. s’il ne pleut pas, je prends mon imperméable

e. aucune des quatre assertions précédentes

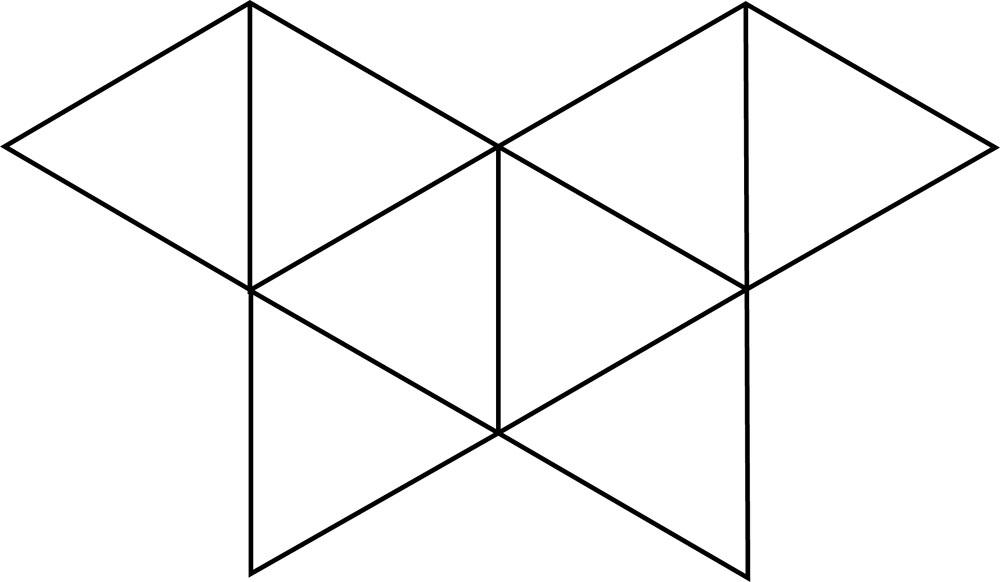
2. Combien de sommets possède le polyèdre convexe dont voici un développement ?

a. 6

b. 8

c. 9

d. 10

e. 12

3. Pablo lit un livre, dont les pages sont numérotées à partir de 1. A un moment où il est en bas d’une page, en additionnant les numéros des pages qu’il a déjà lues, il obtient 351 ; en additionnant les numéros des pages qu’il lui reste à lire, il obtient 469. Combien ce livre a-t-il de pages ?

4. Deux cônes identiques sont posés sur leur base. Avec un litre de peinture, je peins la surface latérale du premier et la partie supérieure de celle du second, jusqu’à mi-hauteur. Combien de peinture (en centilitres) me faut-il pour terminer le deuxième cône ?

a. 33,333…

b. 40

c. 60

d. 66,666…

e. 77,777…

5. La somme des longueurs des trois côtés d’un triangle rectangle vaut 18. La somme des carrés de ces longueurs vaut 128. Que mesure l’aire de ce triangle ?

6. Quatre amis ont apporté chacun un cadeau qu’ils placent dans une corbeille. Ils tirent ensuite au sort pour distribuer les cadeaux. Quelle est la probabilité qu’aucun des quatre amis ne reçoive le cadeau qu’il avait lui-même apporté ?

a. 1/8

b. 1/4

c. 3/8

d. 5/12

e. oe

7. Dans une finale de 100 m, trois des huit coureurs sont Jamaïcains. Combien y a-t-il de podiums (ordonnés) possibles avec exactement un Jamaïcain ?

a. 225

b. 180

c. 56

d. 30

e. 6

8. Quel est le plus grand carré parfait qui soit aussi un cube parfait inférieur à 1 000 ?

9. Je possède entre 100 et 200 billes. Si je les partage en 2, il m’en reste une. Si je les partage en 3, il m’en reste 2. Si je les partage en 4, il m’en reste 3. Enfin, je peux les partager exactement en 5. Combien ai-je de billes ?

Réponses : Niveau mini (1er et 2e secondaires) : 1) 9 ; 2) 20 ; 3) B ; 4) 9 240 ; 5) 12 ; 6) 24 ; 7) 37,5 % ; 8) 44 ; 9) 61 ? Niveau midi (3e et 4e secondaires) : 1) 2. (-0,1)3 ; 2) 59 ; 3) 28 ; 4) Si les notes des élèves sont toutes supérieures à 10, alors la moyenne est supérieure à 10 ; 5) 36 ; 6) 11 ; 7) 1215 ; 8) 23 ; 9) 33 ? Niveau maxi (5e et 6e secondaires) : 1) s’il pleut, je prends mon imperméable ; 2) 6 ; 3) 40 ; 4) 60 ; 5) 9 ; 6) 3/8 ; 7) 180 ; 8) 729 ; 9) 155.